Calculer la recette d’un émail à partir de sa formule n’a rien d’immédiat. Qui s’est appliqué à le faire à la main sait à quel point c’est fastidieux, sauf à simplifier drastiquement la composition des matières premières.
C’est typiquement le genre de calcul qui se prête à l’automatisation. Encore faut-il présenter les choses de telle manière que la mise en équation puisse être traitée par un logiciel.
Détails de la mise en équation, et résolution du système avec Libre Office.
Terminologie
Celle que je vais employer ici n’a rien d’absolu. Je la précise pour qu’on s’entende bien.
Composant
J’appelle composants, ou oxydes, les oxydes qui composent la glaçure. J’ai pris en compte 18 composants, 18 oxydes, qu’on voit apparaître dans le tableau de saisie de la formule.

Ingrédients
J’appelle ingrédients les produits qu’on mélange pour préparer une glaçure. Ce sont les poudres telles qu’achetées chez le marchand.
Les ingrédients contiennent des oxydes en proportions variées, et ces proportions sont connues (fournies par le revendeur).
Mise en équation à partir d'un exemple
Supposons que je veuille réaliser cette formule :
0,6 CaO |
0,6 CaO |
Et que pour la réaliser, je dispose d’un feldspath, de carbonate de chaux, de kaolin et de silice, ingrédients dont la composition molaire est précisée dans un tableau de composition molaire des matières premières :
| Feldspath | Kaolin | Carbonate de chaux | Silice C400 | |
|---|---|---|---|---|
| KNaO | 1 | 0 | 0 | 0 |
| CaO | 0 | 0 | 1 | 0 |
| Al2O3 | 1 | 1 | 0 | 0 |
| SiO2 | 6 | 2 | 0 | 1 |
| Feldspath | Kaolin | Carbonate de chaux | Silice C400 | |
|---|---|---|---|---|
| KNaO | 1 | 0 | 0 | 0 |
| CaO | 0 | 0 | 1 | 0 |
| Al2O3 | 1 | 1 | 0 | 0 |
| SiO2 | 6 | 2 | 0 | 1 |
Ce tableau se lit en colonnes. Ainsi, une mole de feldspath contient 1 mole de KNaO, 0 mole de CaO, 1 mole de Al2O3 et 6 moles de SiO2. Et ainsi de suite.
Mise en équation
Dans le tableau de composition des matières premières, la formule voulue a été ajoutée dans la colonne de droite, et des coefficients multiplicateurs X_{1}, X_{2}, X_{3}, X_{4} ont été ajouté dans la ligne du haut.
| Coefficient multiplicateur | X1 | X2 | X3 | X4 | |
|---|---|---|---|---|---|
| Feldspath | Kaolin | Carbonate de chaux | Silice C400 | Formule voulue | |
| KNaO | 1 | 0 | 0 | 0 | 0,4 KNaO |
| CaO | 0 | 0 | 1 | 0 | 0,6 CaO |
| Al2O3 | 1 | 1 | 0 | 0 | 0,6 Al2O3 |
| SiO2 | 6 | 2 | 0 | 1 | 6 SiO2 |
Trouver la recette revient à déterminer la valeur de ces coefficients.
Pour bien comprendre cette notion de coefficient, on peut dès maintenant déterminer X_{1}, le coefficient multiplicateur du feldspath. Cet ingrédient est le seul à fournir le KNaO, donc si je mettais 1 mole de feldspath, j’aurais 1 mole de KNaO dans ma formule.
Or, il en faut 0,4 mol, on en déduit donc que X_{1}=0,4.
Le coefficient X_{1} étant défini, je sais que le feldspath apportera par ailleurs X_{1} mol d’Al2O3, et 6X_{1} mol de SiO2, soit respectivement 0,4mol et 2,4 mol.
Cette information sera prise en compte pour calculer tous les coefficients suivants.
Mais nous n’allons pas poursuivre la résolution numérique. Notre objectif ici, c’est de faire une mise en équation pour pouvoir étendre notre raisonnement à des recettes plus complexes.
Réalisons un nouveau tableau, dans lequel on applique, pour chaque ingrédient son coefficient multiplicateur.
| Coefficient multiplicateur | X1 | X2 | X3 | X4 | |
| Feldspath | Kaolin | Carbonate de chaux | Silice C400 | Formule voulue | |
| KNaO | X1 | 0 | 0 | 0 | 0,4 KNaO |
| CaO | 0 | 0 | X3 | 0 | 0,6 CaO |
| Al2O3 | X1 | X2 | 0 | 0 | 0,6 Al2O3 |
| SiO2 | 6.X1 | 2.X2 | 0 | X4 | 6 SiO2 |
En lisant ligne par ligne, on comprend que c’est l’addition des quantités de chaque ingrédient qui doit réaliser ce qui se trouve dans la formule. C’est ainsi qu’on écrit, pour la ligne du KNaO :
X_{1}+0+0+0=0,4 soit : X_{1}=0,4
En procédant de même pour les autres lignes, on obtient le système d’équations suivant :
\left\lbrace\begin{array}{llll}X_{1}=0,4\\X_{3}=0,6\\X_{1}+X_{2}=0,6\\6X_{1}+2X_{2}+X{4}=6\end{array}\right.
Sa résolution est simple, on trouve :
\left\lbrace\begin{array}{llll}X_{1}=0,4\\X_{2}=0,2\\X_{3}=0,6\\X_{4}=3,2\end{array}\right.
En reportant ces résultats dans le tableau, on voit immédiatement que le problème est correctement résolu.
| Coefficient multiplicateur | 0,4 | 0,2 | 0,6 | 3,2 | |
| Feldspath | Kaolin | Carbonate de chaux | Silice C400 | Formule | |
| KNaO | 0,4 | 0 | 0 | 0 | 0,4 KNaO |
| CaO | 0 | 0 | 0,6 | 0 | 0,6 CaO |
| Al2O3 | 0,4 | 0,2 | 0 | 0 | 0,6 Al2O3 |
| SiO2 | 2,4 | 0,4 | 0 | 3,2 | 6 SiO2 |
Notre recette sera donc constituée de :
- 0,4 mol de feldspath
- 0,2 mol de kaolin
- 0,6 mol de carbonate de chaux
- 3,2 mole de Silice C400
Il restera à convertir ça en masses, à l’aide des masses molaires de nos ingrédients et de la perte au feu.
Mise en équations sous forme de matrices
Les matrices sont ni plus ni moins des tableaux qu’on peut multiplier entre eux, moyennant quelques règles. L’intérêt de présenter nos calculs en matrices, c’est qu’on pourra se servir de Libre Office pour faire la résolution à notre place.
Reprenons le tableau de composition molaire des matières premières.
| Coefficient multiplicateur | X1 | X2 | X3 | X4 | |
|---|---|---|---|---|---|
| Feldspath | Kaolin | Carbonate de chaux | Silice C400 | Formule voulue | |
| KNaO | 1 | 0 | 0 | 0 | 0,4 KNaO |
| CaO | 0 | 0 | 1 | 0 | 0,6 CaO |
| Al2O3 | 1 | 1 | 0 | 0 | 0,6 Al2O3 |
| SiO2 | 6 | 2 | 0 | 1 | 6 SiO2 |
Appelons matrice M, la partie numérique de ce tableau. M=\begin{pmatrix}1&0&0&0\\0&0&1&0\\1&1&0&0\\6&2&0&1\end{pmatrix}
Mettons les coeficients multiplicateurs sous la forme d’une matrice colonne X (ainsi appelée parce qu’elle n’a qu’une colonne, on l’appellera aussi “vecteur colonne”).
X=\begin{pmatrix}X_{1}\\X_{2}\\X_{3}\\X_{4}\end{pmatrix}
Et enfin, mettons les nombres de moles de la formule sous la forme d’un vecteur colonne qu’on appelle R
R=\begin{pmatrix}R_{1}\\R_{2}\\R_{3}\\R_{4}\end{pmatrix}=\begin{pmatrix}0,4\\0,6\\0,6\\6\end{pmatrix}
C’est là que la magie commence : écrire la partie de gauche du système d’équations précédemment établi
\left\lbrace\begin{array}{llll}X_{1}=0,4\\X_{3}=0,6\\X_{1}+X_{2}=0,6\\6X_{1}+2X_{2}+X{4}=6\end{array}\right.
revient exactement à faire le produit de matrices M\cdot X
Et écrire le système d’équations complet revient à écrire l’équation matricielle M\cdot X=R, c’est à dire
\begin{pmatrix}1&0&0&0\\0&0&1&0\\1&1&0&0\\6&2&0&1\end{pmatrix}\begin{pmatrix}X_{1}\\X_{2}\\X_{3}\\X_{4}\end{pmatrix}=\begin{pmatrix}0,4\\0,6\\0,6\\6\end{pmatrix}
Résolution de l'équation matricielle
Comme c’est le vecteur colonne X qu’on cherche, on aimerait bien “passer la matrice M de l’autre côté” de l’équation.
Rien de plus simple si l’on suppose que la matrice M est inversible, ce que nous admettrons pour le moment. (Nous reviendrons plus tard sur cette hypothèse loin d’être anodine.)
On peut alors écrire, si M^{-1} est la matrice inverse de M :X=M^{-1}\cdot R
Pour avoir notre recette, “il suffit” donc d’inverser la matrice M. C’est là que ça devient vraiment intéressant, parce que Libre Office calc sait inverser les matrices (quand elles sont inversibles, évidemment…), et bien sûr, il sait aussi faire des produits de matrices.
Je demande donc à Libre Office d’inverser la matrice pour moi, et il me donne le résultat suivant :
M^{-1}=\begin{pmatrix}1&0&0&0\\-1&0&1&0\\0&1&0&0\\-4&0&-2&1\end{pmatrix}
Ayant M^{-1}, il nous reste à effectuer le produit M^{-1}\cdot R pour avoir ce qu’on cherche, à savoir notre vecteur colonne X. Je le fais à la main, pour le plaisir 😉 :
\begin{pmatrix}1&0&0&0\\-1&0&1&0\\0&1&0&0\\-4&0&-2&1\end{pmatrix}\begin{pmatrix}0,4\\0,6\\0,6\\6\end{pmatrix}=\begin{pmatrix}1\times0,4+0\times0,6+0\times0,6+0\times6\\-1\times0,4+0\times0,6+1\times0,6+0\times6\\0\times0,4+1\times0,6+0\times0,6+0\times6\\-4\times0,4+0\times0,6-2\times0,6+1\times6\end{pmatrix}
Soit finalement, X=\begin{pmatrix}0,4\\0,2\\0,6\\3,2\end{pmatrix}
Remettons ce résultat en regard de notre tableau de tout à l’heure :
| Coefficient multiplicateur | 0,4 | 0,2 | 0,6 | 3,2 | |
| Feldspath | Kaolin | Carbonate de chaux | Silice C400 | Formule | |
| KNaO | 0,4 | 0 | 0 | 0 | 0,4 KNaO |
| CaO | 0 | 0 | 0,6 | 0 | 0,6 CaO |
| Al2O3 | 0,4 | 0,2 | 0 | 0 | 0,6 Al2O3 |
| SiO2 | 2,4 | 0,4 | 0 | 3,2 | 6 SiO2 |
On retrouve bien les coefficients multiplicateurs que nous avions calculés.
Application au problème général
18 équations et 18 inconnues
Pour notre exemple, nous avons limité le problème à 4 oxydes et 4 ingrédients. Mais pour que le calcul traite tous les cas possibles, il doit prendre en compte les 18 oxydes possiblement contenus dans la formule. Le tableau qu’on a fait dans l’exemple comportera donc 18 lignes au lieu de 4, et le système d’équations qu’on avait écrit et qui comportait 4 lignes, en comportera 18.
On aura donc 18 équations.
C’est maintenant qu’on revient sur l’hypothèse selon laquelle la matrice M est inversible.
Pour qu’elle le soit, il faut :
- Qu’elle soit “carrée”
C’est à dire qu’elle comporte le même nombre de lignes et de colonnes. Pour que ce soit le cas, il faut donc 18 colonnes, c’est à dire 18 coefficients multiplicateurs, c’est à dire 18 ingrédients. - Que ces ingrédients soient “libres” entre eux
C’est à dire qu’on ne puisse pas déduire la composition de l’un en combinant la composition des autres (en corollaire, on ne peut pas mettre deux fois le même ingrédient). - Qu’elle ne comporte aucune ligne nulle
C’est à dire que les ingrédients sont sélectionnés de telle manière que tous les oxydes peuvent être fournis.
Je sais que c’est un peu théorique, mais soyez rassurés si vous ne comprenez pas ce passage, ça n’a pas d’importance pour comprendre la suite. D’un point de vue pratique dans l’utilisation de la page de calcul des recettes, les trois propositions ci-dessus expliquent qu’on utilise exactement 18 ingrédients, et que si on sélectionne deux fois le même via les listes dans la page de calcul, cela renvoie une erreur.
Du coup, avec tout ça, voilà l’allure du tableau qu’on obtient, avec ses 18 lignes et ses 18 colonnes, c’est notre nouvelle matrice M :
| Ingrédients | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
| Na2O | 0,5 | 0,2 | 0,2 | 3 | ||||||||||||||
| K2O | 0,5 | 0,7 | ||||||||||||||||
| CaO | 0,1 | 1 | 0,1 | 0,5 | ||||||||||||||
| MgO | 1 | 0,1 | ||||||||||||||||
| Li2O | 1 | |||||||||||||||||
| ZnO | 1 | |||||||||||||||||
| BaO | 1 | |||||||||||||||||
| CuO | 1 | |||||||||||||||||
| NiO | 1 | |||||||||||||||||
| SrO | 1 | |||||||||||||||||
| Al2O3 | 1 | 0,9 | 1 | |||||||||||||||
| Fe2O3 | 1 | |||||||||||||||||
| B2O3 | 1 | |||||||||||||||||
| SiO2 | 6 | 5 | 1 | 1,5 | 2 | 0,2 | 0,1 | 1 | 0,5 | |||||||||
| TiO2 | 1 | |||||||||||||||||
| SnO2 | 1 | |||||||||||||||||
| ZrO2 | 0,5 | |||||||||||||||||
| P2O5 | 1 | |||||||||||||||||
Dans ce tableau, vous voyez qu’aucune ligne n’est nulle (tous les oxydes ont une matière première pour être fournis), et que les matières premières sont indépendantes entre elles (aucune colonne ne peut être écrite en combinant les autres).
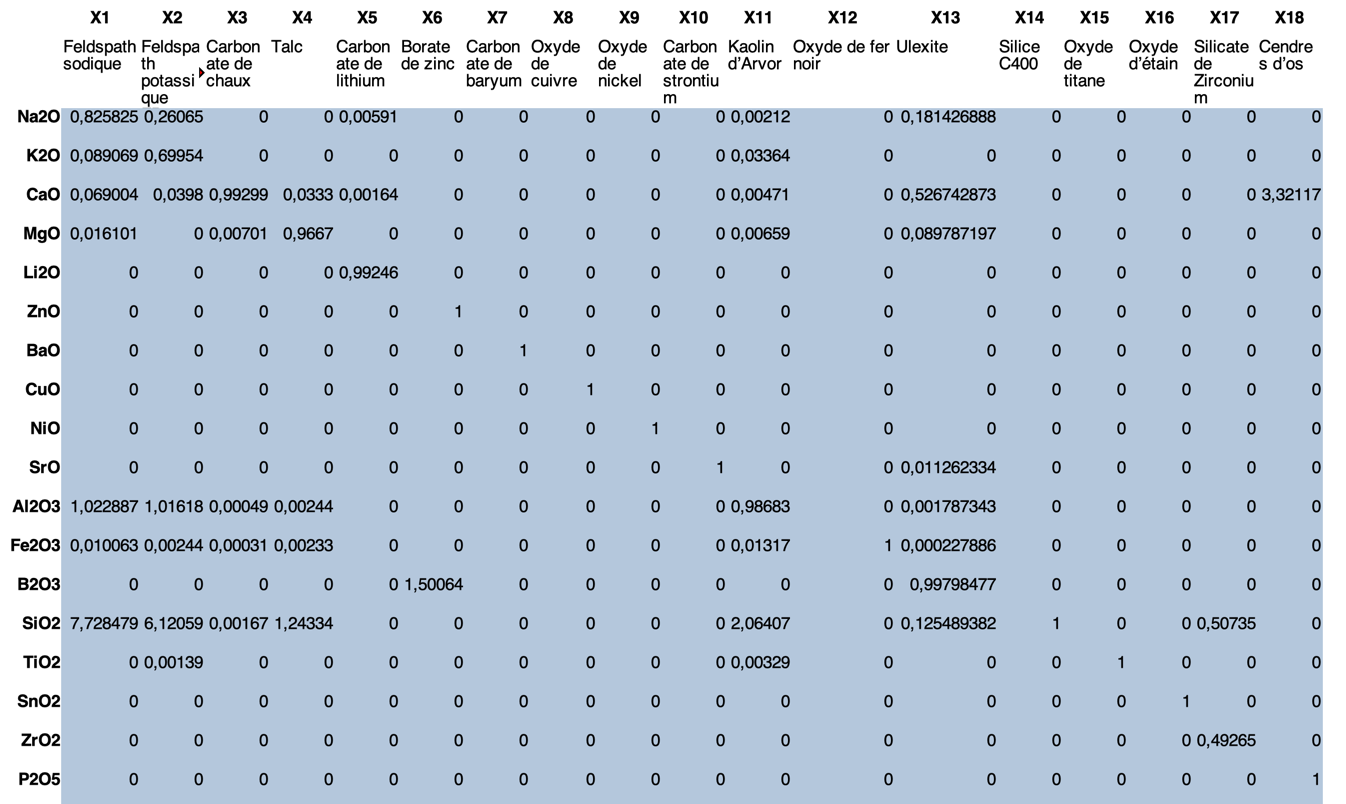
Dans la vraie vie, la composition des matières premières n’est pas aussi simple que dans ce tableau. Pour illustrer cela, voici la table des matières premières qui est utilisée dans le calcul. (Ces 18 matières premières ont été préalablement sélectionnées par l’utilisateur via les listes de sélection.)
Les observateurs concentrés auront remarqué que ce dernier tableau n’est pas écrit dans le même sens que le précédent. Les lignes et les colonnes sont inversées.
Établissement de la matrice M
Cet arrangement de tableau, avec les matières premières en ligne et les oxydes en colonne, présente un intérêt certain : dans la base de données, où sont stockées toutes les données des matières premières, on peut écrire autant de lignes qu’on veut en ajoutant de nouveaux matériaux. S’ils étaient écrits en colonne ça ne serait pas pratique.
Bref ! Quoi qu’il en soit, notre tableau est à l’envers, il faut le remettre à l’endroit pour établir la matrice M.
Rien de plus simple avec Libre Office, qui sait aussi calculer une transposée de matrice 😛 . Avec cette fonction, j’obtiens, dans la page de calcul, la matrice M que voici :
Là, normalement, c’est le moment où tout le monde fait “Wouaaaah” 😮! Moi-même, je suis un peu émue, j’avoue. Ben oui, car nous avançons bien, mine de rien.
La preuve, c’est que pour le reste du calcul, c’est exactement pareil que pour notre exemple. Comme écrit en aide mémoire dans l’entête du tableau ci-dessus,
- X1 est le coefficient multiplicateur du feldspath sodique
- X2 celui du feldspath potassique
- X3 celui du carbonate de chaux,
- …
- X18 celui des cendres d’os
Cette liste des coefficients multiplicateurs correspond au vecteur colonne X, qui contient maintenant 18 éléments, nos 18 inconnues.
X=\begin{pmatrix}X_{1}\\X_{2}\\X_{3}\\X_{4}\\X_{5}\\X_{6}\\X_{7}\\X_{8}\\X_{9}\\X_{10}\\X_{11}\\X_{12}\\X_{13}\\X_{14}\\X_{15}\\X_{16}\\X_{17}\\X_{18}\end{pmatrix}
Par ailleurs, le vecteur R, contient les nombres de moles des 18 oxydes que l’on souhaite dans notre formule. Supposons que l’on veuille la formule ci-dessous.

Alors le vecteur R sera :
R=\begin{pmatrix}0,08\\0,14\\0,49\\0,16\\0\\0,06\\0,07\\0\\0\\0\\0,24\\0\\0,1\\2,83\\0\\0,05\\0\\0\end{pmatrix}
Là où on est rendu, pour avoir le vecteur X, il ne nous reste plus qu’à faire l’opération :M^{-1}\cdot R
Ce que Libre Office Calc va faire pour nous, évidemment. On commence par lui demander de calculer la matrice inverse M^{-1}, que voici :
Puis on lui fait effectuer le produit de matrices M^{-1}\cdot R, ce qui nous donne le résultat suivant :
À ce stade, le lecteur encore réveillé et attentif va remarquer une chose, une chose bien embêtante dont il va falloir s’occuper.
Il y a, parmi les résultats, des valeurs négatives 😱
Eh oui, la résolution de notre système se fait dans l’ensemble des réels, elle peut donc renvoyer des nombres négatifs, et ça, ça ne correspond à rien de réalisable concrètement. (On ne pourra pas enlever de notre mélange de l’oxyde de fer noir, ou de l’oxyde de titane, ou alors il faut une super bonne pince à épiler.)
Bon, vous êtes encore là ? Alors on s’en occupe.
Mise à zéro des valeurs négatives
Comme on ne peut pas mettre une masse négative d’un produit, on va mettre à zéro toutes les valeurs négatives.
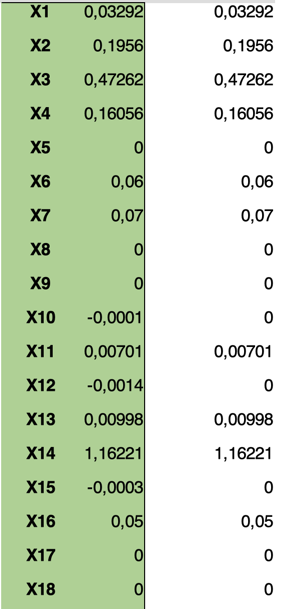
Ce rabotage explique que les résultats ne sont pas toujours exacts quand on cherche une recette. Les écarts seront d’autant plus importants que des valeurs négatives “importantes” seront trouvées par le calcul.
Dans cet exemple, l’incidence est très faible, puisque les valeurs négatives sont toutes petites. La plus grande est X_{12}. C’est le coefficient multiplicateur de l‘oxyde de fer, et on remarque dans le résultat les 0,2% d’erreur qui en découlent (erreur précisée en regard de la case de saisie du Fe2O3).

Le jeu, lorsqu’on cherche une recette, consiste à sélectionner les ingrédients qui, mis ensemble, feront que le vecteur X ne comportera pas de valeurs négatives, et s’il en contient, qu’elles soit aussi proches de zéro que possible.
Cette approche, très simple en pratique, est détaillée dans le tuto optimisez vos recettes de glaçures.
La botte secrète du chef
Mais le calcul n’en reste pas là. Après la mise à zéro des valeurs négatives de X, il analyse si des ajustements peuvent être faits pour s’approcher encore mieux de la formule.
Je ne vais pas développer ça ici, parce que je crois que l’article est déjà suffisamment touffu, mais si cette procédure vous intéresse, laissez-moi un commentaire et je me ferai une joie de détailler cette partie du calcul.
Obtention de la recette en grammes
Ce qui importe dans la recette, ce sont les proportions entre les ingrédients, et ces proportions nous les avons avec notre vecteur X, à cela près que ces proportions sont des proportions entre les nombres de moles après feu de chaque ingrédient.
(Pour les notions de perte au feu et de masses molaires avant et après feu, je vous renvoie à l’article : calcul des masses molaires des matières premières complexes.)
La question est donc : comment convertir ces proportions molaires “après feu” en proportions massiques “avant feu” ?
Qu’on se rassure, c’est simple et rapide, dès qu’on dispose de la masse molaire avant feu de chaque ingrédient (voir l’article cité plus haut pour l’obtention de ces données).
Supposons donc connues m_{1}, la masse molaire avant feu de la matière première n°1 (celle à laquelle est attribué le coefficient X_{1}), m_{2}, celle de la matière première n°2, … etc., jusqu’à m_{18}, la masse molaire après feu de la matière première n°18.
Alors les proportions massiques de la recette seront résumées dans le vecteur colonne :
\begin{pmatrix}m_{1}X_{1}\\m_{2}X_{2}\\m_{3}X_{3}\\m_{4}X_{4}\\m_{5}X_{5}\\m_{6}X_{6}\\m_{7}X_{7}\\m_{8}X_{8}\\m_{9}X_{9}\\m_{10}X_{10}\\m_{11}X_{11}\\m_{12}X_{12}\\m_{13}X_{13}\\m_{14}X_{14}\\m_{15}X_{15}\\m_{16}X_{16}\\m_{17}X_{17}\\m_{18}X_{18}\end{pmatrix}
Cette fois c’est gagné 🤠 , nous avons bel et bien les proportions massiques avant feu des ingrédients.
Il ne reste plus qu’à décider de la quantité qu’on veut préparer, et faire une bonne vieille règle de 3 pour avoir la quantité, en grammes, de chaque ingrédient.
En conclusion
Eh bien bravo 👏 vous êtes arrivés à la fin de cet article.
J’ai voulu être précise, tout en n’étant pas trop théorique, de manière à permettre aux moins “matheux” d’entre vous à comprendre de quoi il s’agit.
J’espère y être parvenue, et si vous avez des questions, des remarques ou des suggestions, laissez un commentaire, j’y répondrai dans la mesure de mes moyens 🤓
Merci de votre attention, et à bientôt 🙃
Calcul des masses molaires
Calculer la masse molaire d’une matière première complexe
Calcul des masses molaires
Calculer la masse molaire d’une matière première complexe